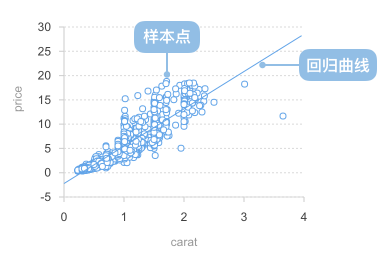
回归曲线图
上一篇
分组柱状图
下一篇
茎叶图
Loading...

回归曲线图是一种在散点图基础上添加回归曲线的统计图表,用于展示两个或多个变量之间的数学关系和预测趋势。回归曲线通过数学算法拟合数据点,找出变量间的最佳函数关系,帮助分析数据的内在规律和进行趋势预测。
回归曲线图结合了散点图的数据分布展示能力和数学建模的预测功能,不仅能直观地显示数据点的分布,还能通过拟合曲线揭示变量间的潜在关系,是数据分析和科学研究中的重要工具。
常见的回归类型包括线性回归、多项式回归、指数回归、对数回归等,不同的回归方法适用于不同的数据模式和关系类型。
英文名:Regression Curve Chart
| 图表类型 | 回归曲线图 |
|---|---|
| 适合的数据 | 两个连续数据字段:一个自变量字段、一个因变量字段 |
| 功能 | 展示变量间的数学关系,识别数据趋势,进行预测分析 |
| 数据与图形的映射 | 自变量字段映射到横轴位置 因变量字段映射到纵轴位置 数据点显示原始观测值 回归曲线显示拟合的数学关系 |
| 适合的数据条数 | 10-1000 条数据,数据点足够多才能有效进行回归分析 |
组成元素:
例子 1: 线性关系数据分析
线性回归适用于展示两个变量之间的线性关系,如身高与体重、温度与销量等。
import { Chart } from '@antv/g2';import { regressionLinear } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});chart.options({type: 'view',autoFit: true,data: {type: 'fetch',value: 'https://assets.antv.antgroup.com/g2/linear-regression.json',},children: [{type: 'point',encode: { x: (d) => d[0], y: (d) => d[1] },scale: { x: { domain: [0, 1] }, y: { domain: [0, 5] } },style: { fillOpacity: 0.75, fill: '#1890ff' },},{type: 'line',data: {transform: [{type: 'custom',callback: regressionLinear(),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: { stroke: '#30BF78', lineWidth: 2 },labels: [{text: 'y = 1.7x + 3.01',selector: 'last',position: 'right',textAlign: 'end',dy: -8,},],tooltip: false,},],axis: {x: { title: '自变量 X' },y: { title: '因变量 Y' },},});chart.render();
说明:
例子 2: 非线性关系 - 二次回归
当数据呈现弯曲趋势时,可以使用二次回归(抛物线)来拟合数据。
import { Chart } from '@antv/g2';import { regressionQuad } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});const data = [{ x: -4, y: 5.2 },{ x: -3, y: 2.8 },{ x: -2, y: 1.5 },{ x: -1, y: 0.8 },{ x: 0, y: 0.5 },{ x: 1, y: 0.8 },{ x: 2, y: 1.5 },{ x: 3, y: 2.8 },{ x: 4, y: 5.2 },];chart.options({type: 'view',autoFit: true,data,children: [{type: 'point',encode: { x: 'x', y: 'y' },style: { fillOpacity: 0.75, fill: '#1890ff' },},{type: 'line',data: {transform: [{type: 'custom',callback: regressionQuad().x((d) => d.x).y((d) => d.y).domain([-4, 4]),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: { stroke: '#30BF78', lineWidth: 2 },labels: [{text: 'y = 0.3x² + 0.5',selector: 'last',textAlign: 'end',dy: -8,},],tooltip: false,},],axis: {x: { title: '自变量 X' },y: { title: '因变量 Y' },},});chart.render();
说明:
例子 3: 指数增长趋势分析
指数回归适用于展示指数增长或衰减的数据模式,如人口增长、细菌繁殖等。
import { Chart } from '@antv/g2';import { regressionExp } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});chart.options({type: 'view',autoFit: true,data: {type: 'fetch',value: 'https://assets.antv.antgroup.com/g2/exponential-regression.json',},children: [{type: 'point',encode: { x: (d) => d[0], y: (d) => d[1] },scale: {x: { domain: [0, 18] },y: { domain: [0, 100000] },},style: { fillOpacity: 0.75, fill: '#1890ff' },},{type: 'line',data: {transform: [{type: 'custom',callback: regressionExp(),},],},encode: {x: (d) => d[0],y: (d) => d[1],shape: 'smooth',},style: { stroke: '#30BF78', lineWidth: 2 },labels: [{text: 'y = 3477.32e^(0.18x)\nR² = 0.998',selector: 'last',textAlign: 'end',dy: -20,},],tooltip: false,},],axis: {x: { title: '时间' },y: {title: '数值',labelFormatter: '~s',},},});chart.render();
说明:
例子 1: 数据点过少的情况
当数据点太少时,回归分析可能不够可靠,容易产生误导性的结论。
import { Chart } from '@antv/g2';import { regressionLinear } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});const insufficientData = [{ x: 1, y: 2 },{ x: 3, y: 4 },{ x: 5, y: 3 },];chart.options({type: 'view',autoFit: true,data: insufficientData,children: [{type: 'point',encode: { x: 'x', y: 'y' },style: {fillOpacity: 0.8,fill: '#ff4d4f',r: 8,},},{type: 'line',data: {transform: [{type: 'custom',callback: regressionLinear().x((d) => d.x).y((d) => d.y),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: {stroke: '#ff4d4f',lineWidth: 2,strokeDasharray: [4, 4],},tooltip: false,},],axis: {x: { title: '变量 X' },y: { title: '变量 Y' },},title: '不适合:数据点过少的回归分析',});chart.render();
问题说明:
例子 2: 无明显相关关系的数据
当两个变量之间没有明显的相关关系时,强行添加回归线可能会误导分析。
import { Chart } from '@antv/g2';import { regressionLinear } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});// 生成随机分布的数据(无相关关系)const randomData = Array.from({ length: 30 }, (_, i) => ({x: Math.random() * 10,y: Math.random() * 10,}));chart.options({type: 'view',autoFit: true,data: randomData,children: [{type: 'point',encode: { x: 'x', y: 'y' },style: {fillOpacity: 0.8,fill: '#ff4d4f',r: 6,},},{type: 'line',data: {transform: [{type: 'custom',callback: regressionLinear().x((d) => d.x).y((d) => d.y),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: {stroke: '#ff4d4f',lineWidth: 2,strokeDasharray: [4, 4],},labels: [{text: 'R² ≈ 0.02 (极低)',selector: 'last',textAlign: 'end',dy: -8,},],tooltip: false,},],axis: {x: { title: '变量 X' },y: { title: '变量 Y' },},title: '不适合:无相关关系的数据',});chart.render();
问题说明:
当数据呈现复杂的弯曲趋势时,可以使用多项式回归来拟合更复杂的曲线。
import { Chart } from '@antv/g2';import { regressionPoly } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});const polynomialData = [{ x: 0, y: 140 },{ x: 1, y: 149 },{ x: 2, y: 159.6 },{ x: 3, y: 159 },{ x: 4, y: 155.9 },{ x: 5, y: 169 },{ x: 6, y: 162.9 },{ x: 7, y: 169 },{ x: 8, y: 180 },];chart.options({type: 'view',autoFit: true,data: polynomialData,children: [{type: 'point',encode: { x: 'x', y: 'y' },style: { fillOpacity: 0.75, fill: '#1890ff' },},{type: 'line',data: {transform: [{type: 'custom',callback: regressionPoly().x((d) => d.x).y((d) => d.y),},],},encode: {x: (d) => d[0],y: (d) => d[1],shape: 'smooth',},style: { stroke: '#30BF78', lineWidth: 2 },labels: [{text: 'y = 0.24x³ - 3.00x² + 13.45x + 139.77\nR² = 0.92',selector: 'last',textAlign: 'end',dx: -8,dy: -20,},],tooltip: false,},],axis: {x: { title: '时间' },y: { title: '数值' },},});chart.render();
说明:
对数回归适用于增长率逐渐减缓的数据模式。
import { Chart } from '@antv/g2';import { regressionLog } from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});chart.options({type: 'view',autoFit: true,data: {type: 'fetch',value: 'https://assets.antv.antgroup.com/g2/logarithmic-regression.json',},children: [{type: 'point',encode: { x: 'x', y: 'y' },scale: { x: { domain: [0, 35] } },style: { fillOpacity: 0.75, fill: '#1890ff' },},{type: 'line',data: {transform: [{type: 'custom',callback: regressionLog().x((d) => d.x).y((d) => d.y).domain([0.81, 35]),},],},encode: {x: (d) => d[0],y: (d) => d[1],shape: 'smooth',},style: { stroke: '#30BF78', lineWidth: 2 },labels: [{text: 'y = 0.881·ln(x) + 4.173\nR² = 0.958',selector: 'last',textAlign: 'end',dy: -20,},],tooltip: false,},],axis: {x: { title: '变量 X' },y: { title: '变量 Y' },},});chart.render();
说明:
可以在同一图表中展示多种回归方法的对比效果。
import { Chart } from '@antv/g2';import {regressionLinear,regressionQuad,regressionPoly,} from 'd3-regression';const chart = new Chart({container: 'container',theme: 'classic',});const comparisonData = [{ x: 1, y: 2.1 },{ x: 2, y: 3.9 },{ x: 3, y: 6.8 },{ x: 4, y: 10.2 },{ x: 5, y: 15.1 },{ x: 6, y: 21.5 },{ x: 7, y: 29.8 },{ x: 8, y: 40.2 },];chart.options({type: 'view',autoFit: true,data: comparisonData,children: [{type: 'point',encode: { x: 'x', y: 'y' },style: {fillOpacity: 0.8,fill: '#1890ff',r: 6,},},// 线性回归{type: 'line',data: {transform: [{type: 'custom',callback: regressionLinear().x((d) => d.x).y((d) => d.y),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: {stroke: '#ff4d4f',lineWidth: 2,strokeDasharray: [4, 4],},tooltip: false,},// 二次回归{type: 'line',data: {transform: [{type: 'custom',callback: regressionQuad().x((d) => d.x).y((d) => d.y),},],},encode: { x: (d) => d[0], y: (d) => d[1] },style: {stroke: '#30BF78',lineWidth: 2,},tooltip: false,},],axis: {x: { title: '变量 X' },y: { title: '变量 Y' },},legends: [{color: {position: 'top',itemMarker: (color, index) => {if (index === 0)return {symbol: 'line',style: { stroke: '#ff4d4f', strokeDasharray: [4, 4] },};if (index === 1)return { symbol: 'line', style: { stroke: '#30BF78' } };},data: [{ color: '#ff4d4f', value: '线性回归' },{ color: '#30BF78', value: '二次回归' },],},},],});chart.render();
说明: